Содержание
Ошибка
- Автомобиль — модели, марки
- Устройство автомобиля
- Ремонт и обслуживание
- Тюнинг
- Аксессуары и оборудование
- Компоненты
- Безопасность
- Физика процесса
- Новичкам в помощь
- Приглашение
- Официоз (компании)
- Пригородные маршруты
- Персоны
- Наши люди
- ТЮВ
- Эмблемы
- А
- Б
- В
- Г
- Д
- Е
- Ё
- Ж
- З
- И
- Й
- К
- Л
- М
- Н
- О
- П
- Р
- С
- Т
- У
- Ф
- Х
- Ц
- Ч
- Ш
- Щ
- Ъ
- Ы
- Ь
- Э
- Ю
- Я
Навигация
- Заглавная страница
- Сообщество
- Текущие события
- Свежие правки
- Случайная статья
- Справка
Личные инструменты
- Представиться системе
Инструменты
- Спецстраницы
Пространства имён
- Служебная страница
Просмотры
Перейти к: навигация,
поиск
Запрашиваемое название страницы неправильно, пусто, либо неправильно указано межъязыковое или интервики название. Возможно, в названии используются недопустимые символы.
Возможно, в названии используются недопустимые символы.
Возврат к странице Заглавная страница.
Если Вы обнаружили ошибку или хотите дополнить статью, выделите ту часть текста статьи, которая нуждается в редакции, и нажмите Ctrl+Enter. Далее следуйте простой инструкции.
Мощность в физике — обозначение, формулы и примеры
Определение мощности
Допустим, нам необходимо убрать урожай пшеницы с поля площадью 100 га. Это можно сделать вручную или с помощью комбайна. Очевидно, что пока человек обработает 1 га площади, комбайн успеет сделать намного больше. В данном случае разница между человеком и техникой — именно то, что называют мощностью. Отсюда вытекает первое определение.
Мощность в физике — это количество работы, которая совершается за единицу времени. |
Рассмотрим другой пример: между точкой А и точкой Б расстояние 15 км, которое человек проходит за 3 часа, а автомобиль может проехать всего за 10 минут. Понятно, что одно и то же количество работы они сделают за разное время. Что показывает мощность в данном случае? Как быстро или с какой скоростью выполняется некая работа.
Понятно, что одно и то же количество работы они сделают за разное время. Что показывает мощность в данном случае? Как быстро или с какой скоростью выполняется некая работа.
В электромеханике эта величина имеет еще одно определение.
Мощность — это скалярная физическая величина, которая характеризует мгновенную скорость передачи энергии от системы к системе или скорость преобразования, изменения, потребления энергии. |
Напомним, что скалярными величинами называются те, значение которых выражается только числом (без вектора направления).
Мощность человека в зависимости от деятельности
Вид деятельности | Мощность, Вт |
|---|---|
Неспешная ходьба | 60–65 |
Бег со скоростью 9 км/ч | 750 |
Плавание со скоростью 50 м/мин | 850 |
Игра в футбол | 930 |
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Запишитесь и участвуйте в розыгрыше 8 уроков
Как обозначается мощность: единицы измерения
В таблице выше вы увидели обозначение в ваттах, и читая инструкции к бытовой технике, можно заметить, что среди характеристик прибора обязательно указано количество ватт. Это единица измерения механической мощности, используемая в международной системе СИ. Она обозначается буквой W или Вт.
Измерение мощности в ваттах было принято в честь шотландского ученого Джеймса Уатта — изобретателя паровой машины. Он стал одним из родоначальников английской промышленной революции.
В физике принято следующее обозначение мощности: 1 Вт = 1 Дж / 1с.
Это значит, что за 1 ватт принята мощность, необходимая для совершения работы в 1 джоуль за 1 секунду.
В каких единицах еще измеряется мощность? Ученые-астрофизики измеряют ее в эргах в секунду (эрг/сек), а в автомобилестроении до сих пор можно услышать о лошадиных силах.
Интересно, что автором этой последней единицы измерения стал все тот же шотландец Джеймс Уатт. На одной из пивоварен, где он проводил свои исследования, хозяин накачивал воду для производства с помощью лошадей. И Уатт выяснил, что 1 лошадь за секунду поднимает около 75 кг воды на высоту 1 метр. Вот так и появилось измерение в лошадиных силах. Правда, сегодня такое обозначение мощности в физике считается устаревшим.
Одна лошадиная сила — это мощность, необходимая для поднятия груза в 75 кг за 1 секунду на 1 метр. 🐴
Единицы измерения | Вт |
|---|---|
1 ватт | 1 |
1 киловатт | 103 |
1 мегаватт | 106 |
1 эрг в секунду | 10-7 |
1 метрическая лошадиная сила | 735,5 |
Подготовка к ОГЭ по физике онлайн поможет снять стресс перед экзаменом и получить высокий балл.
Все формулы мощности
Зная определения, несложно понять формулы мощности, используемые в разных разделах физики — в механике и электротехнике.
В механике
Механическая мощность (N) равна отношению работы ко времени, за которое она была выполнена.
Основная формула:
N = A / t, где A — работа, t — время ее выполнения.
Если вспомнить, что работой называется произведение модуля силы, модуля перемещения и косинуса угла между ними, мы получим формулу измерения работы.
Если направления модуля приложения силы и модуля перемещения объекта совпадают, угол будет равен 0 градусов, а его косинус равен 1. В таком случае формулу можно упростить:
A = F × S
Используем эту формулу для вычисления мощности:
N = A / t = F × S / t = F × V
В последнем выражении мы исходим из того, что скорость (V) равна отношению перемещения объекта на время, за которое это перемещение произошло.
В электротехнике
В общем случае электрическая мощность (P) говорит о скорости передачи энергии. Она равна произведению напряжения на участке цепи на величину тока, проходящего по этому участку.
P = I × U, где I — напряжение, U — сила тока.
В электротехнике существует несколько видов мощности: активная, реактивная, полная, пиковая и т. д. Но это тема отдельного материала, сейчас же мы потренируемся решать задачи на основе общего понимания этой величины. Посмотрим, как найти мощность, используя вышеуказанные формулы по физике.
Задача 1
Допустим, человек поднимает ведро воды из колодца, прикладывая силу 60 Н. Глубина колодца составляет 10 м, а время, необходимое для поднятия — 30 сек. Какова будет мощность человека в этом случае?
Решение:
Найдем вначале величину работы, используя тот факт, что мы знаем расстояние перемещения (глубину колодца 10 м) и приложенную силу 60 Н.
A = F × S = 60 Н × 10 м = 600 Дж
Когда известно значение работы и времени, найти мощность несложно:
N = A / t = 600 Дж / 30 сек = 20 Вт
Ответ: мощность человека при поднятии ведра — 20 ватт.
Задача 2
В комнате включена лампа мощностью 100 Вт. Напряжение домашней электросети — 220 В. Какая сила тока проходит через эту лампу?
Решение:
Мы знаем, что Р = 100 Вт, а U = 220 В.
Поскольку P = I × U, следовательно I = P / U.
I = 100 / 220 = 0,45 А.
Ответ: через лампу пройдет сила тока 0,45 А.
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Вопросы для самопроверки
Что характеризует механическая мощность?
Какие существуют единицы измерения мощности в физике?
Какая из единиц измерения считается устаревшей?
Мощность можно назвать скалярной величиной? Что это означает?
Как из формулы нахождения мощности получить работу?
Какой буквой обозначается мощность в механике, а какой — в электротехнике?
Какую работу производит за 30 минут устройство мощностью 600 Вт?
Как узнать напряжение в сети, если мы знаем мощность подключенного к ней прибора и силу тока, проходящую через прибор?
Если в течение 1 часа автомобиль №1 едет со скоростью 60 км/ч, а автомобиль №2 — со скоростью 90 км/ч, одинаковую ли мощность они развивают в это время?
Допустим, автобус отвез пассажиров из города А в город В за 1 час.
 Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую?
Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую?
10.4 Момент инерции и кинетическая энергия вращения — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Описать различия между вращательной и поступательной кинетической энергией
- Определить физическую концепцию момента инерции в терминах распределения массы относительно оси вращения
- Объясните, как момент инерции твердых тел влияет на их кинетическую энергию вращения
- Использование закона сохранения механической энергии для анализа систем, подвергающихся как вращению, так и поступательному перемещению
- Расчет угловой скорости вращающейся системы при наличии потерь энергии из-за неконсервативных сил
До сих пор в этой главе мы работали с кинематикой вращения: описанием движения вращающегося твердого тела с фиксированной осью вращения. В этом разделе мы определяем две новые величины, полезные для анализа свойств вращающихся объектов: момент инерции и кинетическую энергию вращения. Определив эти свойства, мы получим два важных инструмента, необходимых для анализа динамики вращения.
В этом разделе мы определяем две новые величины, полезные для анализа свойств вращающихся объектов: момент инерции и кинетическую энергию вращения. Определив эти свойства, мы получим два важных инструмента, необходимых для анализа динамики вращения.
Кинетическая энергия вращения
Любой движущийся объект обладает кинетической энергией. Мы знаем, как вычислить это для тела, совершающего поступательное движение, но как насчет твердого тела, совершающего вращательное движение? Это может показаться сложным, потому что каждая точка твердого тела имеет разную скорость. Однако мы можем использовать угловую скорость, которая одинакова для всего твердого тела, чтобы выразить кинетическую энергию вращающегося объекта. На рис. 10.17 показан пример очень энергичного вращающегося тела: электрический точильный камень, приводимый в движение двигателем. Когда точильный камень выполняет свою работу, летят искры, возникают шум и вибрация. Эта система обладает значительной энергией, частично в виде тепла, света, звука и вибрации. Однако большая часть этой энергии находится в форме кинетической энергии вращения.
Однако большая часть этой энергии находится в форме кинетической энергии вращения.
Рисунок
10.17
Кинетическая энергия вращения точильного камня преобразуется в тепло, свет, звук и вибрацию. (кредит: Закари Дэвид Белл, ВМС США)
Энергия вращательного движения не является новой формой энергии; скорее, это энергия, связанная с вращательным движением, такая же, как кинетическая энергия при поступательном движении. Однако, поскольку кинетическая энергия определяется выражением K=12mv2K=12mv2, а скорость — это величина, разная для каждой точки тела, вращающегося вокруг оси, имеет смысл найти способ записать кинетическую энергию через переменную ωω , который одинаков для всех точек на твердом вращающемся теле. Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение vt=ωrvt=ωr, где r — расстояние частицы от оси вращения, а vtvt — ее тангенциальная скорость. Подставляя в уравнение кинетической энергии, находим
Подставляя в уравнение кинетической энергии, находим
K=12mvt2=12m(ωr)2=12(mr2)ω2.K=12mvt2=12m(ωr)2=12(mr2)ω2.
В случае твердого вращающегося тела мы можем разделить любое тело на большое количество меньших масс, каждая с массой mjmj и расстоянием до оси вращения rjrj, так что полная масса тела равна сумма отдельных масс: M=∑jmjM=∑jmj. Каждая меньшая масса имеет тангенциальную скорость vjvj, где мы опустили нижний индекс 9.0027 т на данный момент. Полная кинетическая энергия твердого вращающегося тела равна
К=∑j12mjvj2=∑j12mj(rjωj)2K=∑j12mjvj2=∑j12mj(rjωj)2
, а поскольку ωj=ωωj=ω для всех масс,
К=12(∑jmjrj2)ω2.K=12(∑jmjrj2)ω2.
10.16
Единицами уравнения 10.16 являются джоули (Дж). Уравнение в этой форме полное, но неудобное; нам нужно найти способ обобщить его.
Момент инерции
Если мы сравним уравнение 10.16 с тем, как мы записали кинетическую энергию в работе и кинетической энергии, (12mv2)(12mv2), это предполагает, что у нас есть новая вращательная переменная, которую нужно добавить в наш список отношений между вращательными и поступательными переменными. Величина ∑jmjrj2∑jmjrj2 соответствует массе в уравнении для кинетической энергии вращения. Это важный новый термин для вращательного движения. Эта величина называется моментом инерции I , с единицами кг·м2 кг·м2:
Величина ∑jmjrj2∑jmjrj2 соответствует массе в уравнении для кинетической энергии вращения. Это важный новый термин для вращательного движения. Эта величина называется моментом инерции I , с единицами кг·м2 кг·м2:
I=∑jmjrj2.I=∑jmjrj2.
10.17
Пока оставим выражение в виде суммирования, представляющее момент инерции системы точечных частиц, вращающихся вокруг неподвижной оси. Заметим, что момент инерции отдельной точечной частицы относительно неподвижной оси равен просто mr2mr2, где r — это расстояние от точечной частицы до оси вращения. В следующем разделе мы исследуем интегральную форму этого уравнения, которую можно использовать для расчета момента инерции некоторых твердых тел правильной формы.
Момент инерции есть количественная мера инерции вращения, как и в поступательном движении, а масса есть количественная мера линейной инерции, т. е. чем массивнее объект, тем больше у него инерция и тем больше его сопротивление изменению линейной скорости. Аналогично, чем больше момент инерции твердого тела или системы частиц, тем больше их сопротивление изменению угловой скорости относительно неподвижной оси вращения. Интересно посмотреть, как меняется момент инерции в зависимости от r, расстояние до оси вращения массовых частиц в уравнении 10.17. Твердые тела и системы частиц с большей массой, сосредоточенные на большем расстоянии от оси вращения, обладают большими моментами инерции, чем тела и системы той же массы, но сосредоточенные вблизи оси вращения. Таким образом, мы можем видеть, что полый цилиндр имеет большую инерцию вращения, чем сплошной цилиндр той же массы при вращении вокруг оси, проходящей через центр. Подставляя уравнение 10.17 в уравнение 10.16, выражение для кинетической энергии вращающегося твердого тела принимает вид
Аналогично, чем больше момент инерции твердого тела или системы частиц, тем больше их сопротивление изменению угловой скорости относительно неподвижной оси вращения. Интересно посмотреть, как меняется момент инерции в зависимости от r, расстояние до оси вращения массовых частиц в уравнении 10.17. Твердые тела и системы частиц с большей массой, сосредоточенные на большем расстоянии от оси вращения, обладают большими моментами инерции, чем тела и системы той же массы, но сосредоточенные вблизи оси вращения. Таким образом, мы можем видеть, что полый цилиндр имеет большую инерцию вращения, чем сплошной цилиндр той же массы при вращении вокруг оси, проходящей через центр. Подставляя уравнение 10.17 в уравнение 10.16, выражение для кинетической энергии вращающегося твердого тела принимает вид
К=12Iω2.K=12Iω2.
10.18
Из этого уравнения видно, что кинетическая энергия вращающегося твердого тела прямо пропорциональна моменту инерции и квадрату угловой скорости. Это используется в устройствах накопления энергии маховика, которые предназначены для накопления большого количества кинетической энергии вращения. Многие автопроизводители в настоящее время испытывают в своих автомобилях накопители энергии маховика, такие как маховик или система рекуперации кинетической энергии, показанные на рис. 10.18.
Это используется в устройствах накопления энергии маховика, которые предназначены для накопления большого количества кинетической энергии вращения. Многие автопроизводители в настоящее время испытывают в своих автомобилях накопители энергии маховика, такие как маховик или система рекуперации кинетической энергии, показанные на рис. 10.18.
Рисунок
10.18
Маховик KERS (система рекуперации кинетической энергии), используемый в автомобилях. (кредит: «cmonville»/Flickr)
Вращательные и поступательные величины кинетической энергии и инерции приведены в таблице 10.4. Столбец отношения не включен, поскольку не существует константы, на которую можно было бы умножить вращательную величину, чтобы получить поступательную величину, как это можно сделать для переменных в таблице 10.3.
| Поворотный | Трансляционное |
|---|---|
| I=∑jmjrj2I=∑jmjrj2 | мм |
| К=12Iω2K=12Iω2 | К=12мв2К=12мв2 |
Стол
10. 4
4
Вращательная и поступательная кинетическая энергия и инерция
Пример
10,8
Момент инерции системы частиц
На стержне ничтожной массы и длины 0,5 м на расстоянии 10 см друг от друга расположены шесть маленьких шайб. Масса каждой шайбы 20 г. Стержень вращается вокруг оси, расположенной на расстоянии 25 см, как показано на рис. 10.19.. а) Чему равен момент инерции системы? б) Если убрать две ближние к оси шайбы, каков будет момент инерции оставшихся четырех шайб? в) Если система с шестью шайбами вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
Рисунок
10.19
Шесть шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы, вращающемся вокруг вертикальной оси.
Стратегия
- Мы используем определение момента инерции для системы частиц и выполняем суммирование для оценки этой величины.
 Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования.
Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования. - Делаем аналогичный расчет.
- Подставляем результат (а) в выражение для кинетической энергии вращения.
Раствор
- I=∑jmjrj2=(0,02 кг)(2×(0,25 м)2+2×(0,15 м)2+2×(0,05 м)2)=0,0035 кг·м2I=∑jmjrj2=( 0,02 кг)(2×(0,25 м)2+2×(0,15 м)2+2×(0,05 м)2)=0,0035 кг·м2.
- I=∑jmjrj2=(0,02 кг)(2×(0,25 м)2+2×(0,15 м)2)=0,0034 кг·м2I=∑jmjrj2=(0,02 кг)(2×(0,25 м)2+2 ×(0,15 м)2)=0,0034 кг·м2.
- K=12Iω2=12(0,0035кг·м2)(5,0×2πрад/с)2=1,73JK=12Iω2=12(0,0035кг·м2)(5,0×2πрад/с)2=1,73Дж.
Значение
Мы можем видеть индивидуальные вклады в момент инерции. Массы вблизи оси вращения вносят очень небольшой вклад. Когда мы их убрали, это очень мало повлияло на момент инерции.
В следующем разделе мы обобщим уравнение суммирования для точечных частиц и разработаем метод расчета моментов инерции твердых тел. Однако пока на рис. 10.20 приведены значения инерции вращения для обычных форм объектов вокруг заданных осей.
Однако пока на рис. 10.20 приведены значения инерции вращения для обычных форм объектов вокруг заданных осей.
Рисунок
10.20
Значения инерции вращения для обычных форм объектов.
Применение кинетической энергии вращения
Теперь давайте применим идеи вращательной кинетической энергии и таблицу моментов инерции, чтобы получить представление об энергии, связанной с несколькими вращающимися объектами. Следующие примеры также помогут вам освоиться с этими уравнениями. Во-первых, давайте рассмотрим общую стратегию решения проблем с вращательной энергией.
Стратегия решения проблем
Энергия вращения
- Определите, какая энергия или работа связана с вращением.
- Определить интересующую систему. Эскиз обычно помогает.
- Проанализируйте ситуацию, чтобы определить виды работы и энергии.
- Если нет потерь энергии на трение и другие неконсервативные силы, механическая энергия сохраняется, т.
 е. Ki+Ui=Kf+UfKi+Ui=Kf+Uf.
е. Ki+Ui=Kf+UfKi+Ui=Kf+Uf. - Если присутствуют неконсервативные силы, механическая энергия не сохраняется, и другие формы энергии, такие как тепло и свет, могут входить в систему или выходить из нее. Определите, каковы они, и рассчитайте их по мере необходимости.
- Удалите термины везде, где это возможно, чтобы упростить алгебру.
- Оцените численное решение, чтобы увидеть, имеет ли оно смысл в физической ситуации, представленной в формулировке задачи.
Пример
10,9
Расчет энергии вертолета
Типичный небольшой спасательный вертолет имеет четыре лопасти: каждая имеет длину 4,00 м и массу 50,0 кг (рис. 10.21). Лопасти можно представить как тонкие стержни, которые вращаются вокруг одного конца оси, перпендикулярной их длине. Вертолет имеет полную загруженную массу 1000 кг. а) Рассчитайте кинетическую энергию вращения лопастей, когда они вращаются со скоростью 300 об/мин. (b) Рассчитайте поступательную кинетическую энергию вертолета, когда он летит со скоростью 20,0 м/с, и сравните ее с энергией вращения лопастей.
(b) Рассчитайте поступательную кинетическую энергию вертолета, когда он летит со скоростью 20,0 м/с, и сравните ее с энергией вращения лопастей.
Рисунок
10.21
(а) Эскиз четырехлопастного вертолета. b) спасательная операция на воде с участием вертолета Оклендской спасательной вертолетной службы Westpac. (кредит b: модификация работы «111 Emergency»/Flickr)
Стратегия
Вращательная и поступательная кинетическая энергия может быть рассчитана по их определениям. Формулировка задачи дает все необходимые константы для вычисления выражений для вращательной и поступательной кинетических энергий.
Решение
- Кинетическая энергия вращения
К=12Iω2.K=12Iω2.
Мы должны преобразовать угловую скорость в радианы в секунду и вычислить момент инерции, прежде чем мы сможем найти K . Угловая скорость ωω равна
ω=300об1,00мин2πрад1 об1,00мин60,0с=31,4рад.
 ω=300об1,00мин2πрад1 об1,00мин60,0с=31,4рад.
ω=300об1,00мин2πрад1 об1,00мин60,0с=31,4рад.Момент инерции одной лопасти равен моменту инерции тонкого стержня, вращающегося вокруг своего конца, как показано на рис. 10.20. Сумма I в четыре раза больше этого момента инерции, потому что лопастей четыре. Таким образом,
I=4Ml23=4×(50,0 кг)(4,00 м)23=1067,0 кг·м2.I=4Ml23=4×(50,0 кг)(4,00 м)23=1067,0 кг·м2.
Ввод ωω и I в выражение для кинетической энергии вращения дает
K=0,5(1067 кг·м2)(31,4 рад/с)2=5,26×105 Дж. K=0,5(1067 кг·м2)(31,4 рад/с)2=5,26×105 Дж.
- Подставляя данные значения в уравнение для поступательной кинетической энергии, получаем
K=12mv2=(0,5)(1000,0 кг)(20,0 м/с)2=2,00×105 Дж. K=12mv2=(0,5)(1000,0 кг)(20,0 м/с)2=2,00×105 Дж.
Для сравнения кинетических энергий мы берем отношение кинетической энергии поступательного движения к кинетической энергии вращения. Это соотношение
2,00×105J5,26×105J=0,380,2,00×105J5,26×105J=0,380.

Значение
Отношение поступательной энергии к кинетической энергии вращения составляет всего 0,380. Это соотношение говорит нам о том, что большая часть кинетической энергии вертолета приходится на его вращающиеся лопасти.
Пример
10.10
Энергия в бумеранге
Человек подбрасывает в воздух бумеранг со скоростью 30,0 м/с под углом 40,0°40,0° к горизонту (рис. 10.22). Он имеет массу 1,0 кг и вращается со скоростью 10,0 об/с. Момент инерции бумеранга равен I=112mL2I=112mL2, где L=0,7mL=0,7м. а) Чему равна полная энергия бумеранга, когда он покидает руку? б) На какую высоту поднимется бумеранг от высоты руки, если пренебречь сопротивлением воздуха?
Рисунок
10.22
Бумеранг брошен в воздух под начальным углом 40°40°.
Стратегия
Мы используем определения вращательной и линейной кинетической энергии, чтобы найти полную энергию системы. Задача состоит в том, чтобы пренебречь сопротивлением воздуха, поэтому нам не нужно беспокоиться о потерях энергии. В части (b) мы используем закон сохранения механической энергии, чтобы найти максимальную высоту бумеранга.
Задача состоит в том, чтобы пренебречь сопротивлением воздуха, поэтому нам не нужно беспокоиться о потерях энергии. В части (b) мы используем закон сохранения механической энергии, чтобы найти максимальную высоту бумеранга.
Раствор
- Момент инерции: I=112 мл2=112(1,0 кг)(0,7 м)2=0,041 кг·м2I=112 мл2=112(1,0 кг)(0,7 м)2=0,041 кг·м2.
Угловая скорость: ω=(10,0об/с)(2π)=62,83рад/сω=(10,0об/с)(2π)=62,83рад/с.
Таким образом, кинетическая энергия вращения равнаKR=12(0,041кг·м2)(62,83рад/с)2=80,93Дж.KR=12(0,041кг·м2)(62,83рад/с)2=80,93Дж.
Поступательная кинетическая энергия
КТ=12мв2=12(1,0кг)(30,0м/с)2=450,0Дж.КТ=12мв2=12(1,0кг)(30,0м/с)2=450,0Дж.
Таким образом, полная энергия бумеранга равна
KTotal=KR+KT=80,93+450,0=530,93J.KTotal=KR+KT=80,93+450,0=530,93J.
- Мы используем закон сохранения механической энергии. Поскольку бумеранг запускается под углом, нам нужно записать полные энергии системы через ее линейные кинетические энергии, используя скорость в x — и y — направления.
 Полная энергия, когда бумеранг покидает руку, равна
Полная энергия, когда бумеранг покидает руку, равнаEBefore=12mvx2+12mvy2+12Iω2.EBefore=12mvx2+12mvy2+12Iω2.
Полная энергия на максимальной высоте равна
EFinal=12mvx2+12Iω2+mgh.EFinal=12mvx2+12Iω2+mgh.
По закону сохранения механической энергии EBefore=EFinalEBefore=EFinal, поэтому после сокращения подобных членов мы имеем
12mvy2=мгх.12mvy2=мгх.
Поскольку vy=30,0 м/с(sin40°)=19,28 м/svy=30,0 м/с(sin40°)=19,28 м/с, находим
ч=(190,28 м/с)22(9,8 м/с2)=18,97 м.ч=(19,28 м/с)22(9,8 м/с2)=18,97 м.
Значение
В части (b) решение демонстрирует, как сохранение энергии является альтернативным методом решения проблемы, которая обычно решается с использованием кинематики. При отсутствии сопротивления воздуха кинетическая энергия вращения не учитывалась в решении для максимальной высоты.
Проверьте свое понимание
10.4
Винт атомной подводной лодки имеет момент инерции 800,0 кг·м2800,0 кг·м2. Если погружной гребной винт имеет скорость вращения 4,0 об/с при выключенном двигателе, какова будет скорость вращения гребного винта через 5,0 с, когда сопротивление воды уберет из системы 50 000 Дж?
Если погружной гребной винт имеет скорость вращения 4,0 об/с при выключенном двигателе, какова будет скорость вращения гребного винта через 5,0 с, когда сопротивление воды уберет из системы 50 000 Дж?
WHAT’S Technical Articles and Product Descriptions Mechanical Engineering FundamentalsPiston Reference Materials EPI Additional Products Stuff
Журнал Race Engine Technology ВВЕДЕНИЕ в Race Engine TechnologyПОДПИСАТЬСЯ
Последнее обновление: | Последнее обновление: 11 марта 2011 г. ПРИМЕЧАНИЕ. Все наши продукты, конструкции и услуги являются УСТОЙЧИВЫМИ, ОРГАНИЧЕСКИМИ, БЕЗГЛЮТЕНОВЫМИ, НЕ СОДЕРЖАТ ГМО и не будут |

 Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую?
Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую? Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования.
Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования. е. Ki+Ui=Kf+UfKi+Ui=Kf+Uf.
е. Ki+Ui=Kf+UfKi+Ui=Kf+Uf.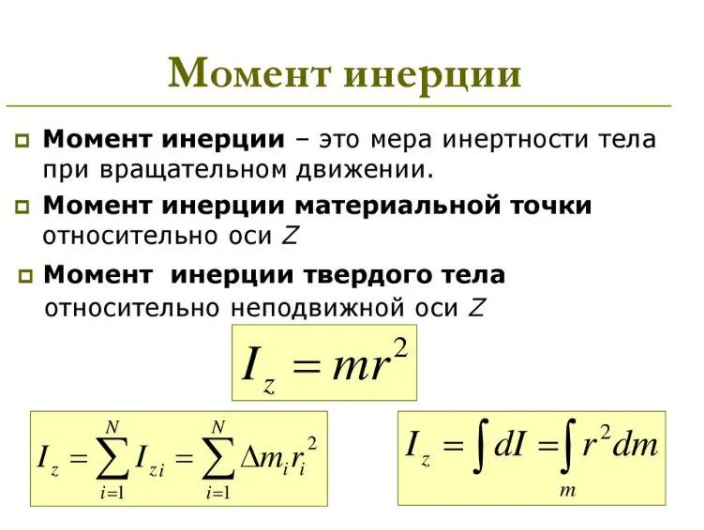 ω=300об1,00мин2πрад1 об1,00мин60,0с=31,4рад.
ω=300об1,00мин2πрад1 об1,00мин60,0с=31,4рад.
 Полная энергия, когда бумеранг покидает руку, равна
Полная энергия, когда бумеранг покидает руку, равна
